2023年安徽专升本公共课《高等数学》考试大纲

Ⅰ.考核目标

普通高校专升本统考科目《高等数学》主要考查考生的数学 知识水平和应用能力.按本说明的要求，考生应掌握微积分、线性代数和概率论的基本概念、基本理论和基本方法 .考生应 具有一定的抽象思维能力、逻辑推理能力、运算能力和空间 想象能力；能运用基本概念、基本理论和基本方法进行推理、证明和计算；能运用所学知识分析并解决简单的实际问题 .

Ⅱ.考试内容

一、微积分

(一)函数、极限与连续

1. 函数的概念 、性质及其应用.

2.反函数、分段函数、复合函数与隐函数.                          

3.基本初等函数的性质与图形，  初等函数的概念.               

4.数列极限、函数极限的概念及性质，极限的四则运算法则.

5.无穷小量与无穷大量的概念，无穷小量的性质，无穷小量 与无穷大量的关系，无穷小量的比较与等价替换 .

6.极限存在准则，两个重要极限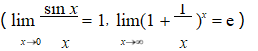

及其简单应用.

7. 函数连续性的概念，函数的间断点及其类型.

8.初等函数的连续性及其应用.

9.闭区间上连续函数的性质.

(二)导数与微分

1.导数的概念及其几何意义， 左导数与右导数的定义，函数的可导性与连续性的关系.

2. 曲线上一点处的切线方程与法线方程.

3.导数的基本公式，函数的四则运算的求导法则，复合函数的求导法则，分段函数和隐函数的导数.

4.高阶导数的概念，简单函数的高阶导数 .

5.微分的概念，可微与可导的关系，基本初等函数的微分公 式，函数的四则运算的微分法则， 复合函数的微分法则.

(三)导数的应用

1.罗尔 (Rolle)  中值定理、拉格朗日 (Lagrange)  中值定理 及其应用.

2.洛必达(L’Hospital)法则及其在未定式极限计算中的应用.

3. 函数的单调性的判定.

4. 函数的极值和最值及其求法.

5. 曲线的凹凸性与拐点的概念及判定.

(四)不定积分

1.不定积分的概念与性质，原函数存在定理.

2.不定积分的基本公式.

3.第一类换元法与第二类换元法.

4.分部积分法.

5.简单有理函数的积分.

(五)定积分

1.定积分的概念与性质.

2.变上限积分函数及其导数，微积分基本定理 .

3.定积分的换元积分法与分部积分法.

4.无穷区间上的广义积分.

5.定积分的应用：  平面图形的面积及平面图形绕坐标轴旋转 一周所得旋转体的体积的计算.

(六)多元函数的微积分

1. 多元函数的概念，二元函数的极限、连续的概念及其基本 性质.

2. 多元函数的一阶、二阶偏导数.                        

3. 多元函数的全微分.                                         

4. 多元复合函数的求导法则与隐函数的求导公式. 

5.二重积分的概念与性质.

6.直角坐标系下与极坐标系下二重积分的计算 .

二、线性代数

( 七 )行列式                        1.行列式的概念与性质.          2.行列式按行(列)展开定理. 3.克莱姆 ( Cramer ) 法则.

(八)矩阵

1.矩阵的概念，  几种特殊的矩阵.

2.矩阵的线性运算、乘法、转置以及它们的运算规律，  方阵 的幂与方阵的行列式.

3.矩阵可逆的概念和性质， 矩阵可逆的判定，逆矩阵的求解， 伴随矩阵的概念.

4.矩阵的秩的概念及其计算.

5.简单矩阵方程的求解.

6.矩阵初等变换与初等矩阵的概念和性质，矩阵的等价 .

(九)线性方程组

1.n 维向量、向量组的线性组合与线性表示的概念，向量组 线性相关性的概念和性质，向量组线性相关性的判定.

2. 向量组的极大线性无关组和向量组的秩的概念，  矩阵的秩 与其行(列)向量组的秩之间的关系.

3.齐次线性方程组有非零解的判定，  非齐次线性方程组有解 的判定.

4.线性方程组的解法以及解的结构.

三、概率论

(十)随机事件及其概率                                      

1.样本空间与随机事件的概念.                               

2.不可能事件与必然事件，事件之间的关系和运算. 

3.概率的统计定义和基本性质，概率的加法公式.   

4.古典概型的定义与事件的概率.

5.条件概率的定义，  概率的乘法公式、全概率公式与贝叶斯  (Bayes) 公式.

6.事件的独立性.

(十 一 )  随机变量及其数字特征

1.随机变量以及随机变量分布函数的概念和性质，  简单随机 变量的分布函数.

2.离散型随机变量及其概率分布.

3.连续型随机变量及其概率分布.

4.一维随机变量的数字特征(数学期望、方差) 的定义、性 质及其求法.

Ⅲ.考试形式与试卷结构

考试形式：闭卷、笔试 .

考试分数：  满分 150 分.

考试时间：  120 分钟.

试卷内容比例：  微积分约 占 60%，  线性代数约占 20%，  概 率论约 占 20% .

试卷题型及分值分布：  选择题共 12 题，  每小题  4 分，  共 48 分；  填空题共 6 题，  每小题  4  分，  共 24 分；  计算题、 证明题、应用题共 7 题，  共 78 分 .