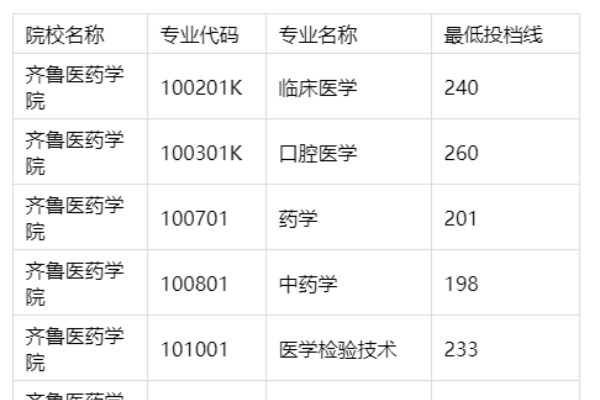
近日齐鲁医药学院发布2023年普通高等教育专科升本科专业综合测试考试大纲，以下为《高等数学 II》科目考试大纲，备考生一起来看看吧~

一、考试题型和分值

( 一) 考试题型:单项选择题、多项选择题等

(二) 总分:100 分

二、参考教材

《高等数学》上下册，高等教育出版社，第 7 版，主编 同济大学数学系

三、考试范围

(一) 函数、极限与连续 1.函数

函数的定义域，函数表达式，函数值。

函数的有界性、单调性、周期性和奇偶性。

分段函数、反函数、复合函数、成本函数、收益函数、利润函数、需 求函数和供给函数

函数的复合运算，初等函数的性质及图形。

要求：

(1) 理解函数的概念，会求函数的定义域、表达式及函数值，会建 立应用问题的函数关系。

(2) 掌握函数的有界性、单调性、周期性和奇偶性。

(3) 理解分段函数、反函数和复合函数的概念。

(4) 掌握函数的四则运算与复合运算。

(5) 掌握基本初等函数的性质及图形，理解初等函数的概念。

(6) 理解经济学中的几种常见函数 (成本函数、收益函数、利润函 数、需求函数和供给函数) 。

2.极限

数列极限和函数极限的概念，两个重要极限，无穷小量、无穷大量的 概念。

数列极限和函数极限的性质、极限的运算法则。

无穷小量的性质，无穷小量阶的比较。

要求：

(1) 理解数列极限和函数极限(包括左极限和右极限)的概念。理解 函数极限存在与左极限、右极限存在之间的关系。

(2) 理解数列极限和函数极限的性质。熟练掌握数列极限和函数极 限的运算法则。

(3) 熟练掌握两个重要极限，并会用它们求极限。

(4) 理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷 小量与无穷大量的关系。会比较无穷小量的阶(高阶、低阶、同阶和等价)。 会用等价无穷小量求极限。

3.连续

连续性的概念，间断点的定义及分类。

闭区间上连续函数的性质。

要求：

(1) 理解函数连续性 (包括左连续和右连续) 的概念，掌握函数 连续与左连续、右连续之间的关系。会求函数的间断点并判断其类型。

(2) 掌握连续函数的四则运算和复合运算。理解初等函数在其定 义区间内的连续性。

(3) 会利用连续性求极限。

(4) 掌握闭区间上连续函数的性质 (有界性定理、最大值和最小 值定理、介值定理、零点定理) ，并会应用这些性质解决相关问题。

(二) 一元函数微分学

1.导数与微分

导数的概念，导数的几何意义，高阶导数的概念，微分的概念，隐函 数求导。

导数的四则运算法则，复合函数的求导法则，基本初等函数的导数公

式，导数与微分的关系。

要求：

(1) 理解导数的概念及几何意义，会用定义求函数在一点处的导数 (包括左导数和右导数) 。会求平面曲线的切线方程和法线方程。理解函 数的可导性与连续性之间的关系。

(2) 熟练掌握导数的四则运算法则和复合函数的求导法则，熟练掌 握基本初等函数的导数公式。

(3) 掌握隐函数求导法、对数求导法。

(4) 理解高阶导数的概念，会求函数的高阶导数。

(5) 理解微分的概念，理解导数与微分的关系，掌握微分运算法则， 会求函数的一阶微分。

2.中值定理及导数的应用

罗尔定理、拉格朗日中值定理，洛必达法则。

驻点、极值点和极值的概念，曲线的凹凸性、拐点以及渐近线的概念， 边际函数、弹性函数。

导数判断函数的单调性和凹凸性，求极值、最值。

要求：

(1) 理解罗尔定理、拉格朗日中值定理。会用罗尔定理和拉格朗日 中值定理解决相关问题。

(2) 熟练掌握洛必达法则，会用洛必达法则求型未定式的极限。

(3) 理解驻点、极值点和极值的概念，掌握用导数判断函数的单调 性和求函数极值的方法，会利用函数的单调性证明不等式，掌握函数最大 值和最小值的求法及其应用。

(4) 会用导数判断曲线的凹凸性，会求曲线的拐点以及水平渐近线 与垂直渐近线。

(5) 理解边际函数、弹性函数的概念及其实际意义，会求解简单的 应用问题。

(三) 一元函数积分学

1.不定积分

原函数的定义，不定积分的概念，不定积分的基本公式。 换元积分法、分部积分法。

要求：

(1) 理解原函数与不定积分的概念，了解原函数存在定理， 掌握不

定积分的性质。

(2) 熟练掌握不定积分的基本公式。

(3) 熟练掌握不定积分的换元积分法和分部积分法。

(4) 掌握简单有理函数的不定积分的求法。

2.定积分

定积分的概念，牛顿-莱布尼茨公式。

定积分的换元积分法与分部积分法。

定积分的应用。

要求：

(1) 理解定积分的概念及几何意义，了解可积的条件。

(2) 掌握定积分的性质及其应用。

(3)理解积分上限的函数，会求它的导数，掌握牛顿-莱布尼茨公式。

(4) 熟练掌握定积分的换元积分法与分部积分法。

(5) 会用定积分表达和计算平面图形的面积、旋转体的体积。

(6) 会利用定积分求解经济分析中的简单应用问题。

(四) 多元函数微积分学 1.多元函数微分学

二元函数的概念，二元函数的极限与连续的概念，二元函数偏导数和 全微分。

隐函数的一阶偏导数的计算方法。

二元函数的极值。

要求：

(1) 理解二元函数的概念、几何意义及二元函数的极限与连续的概 念，会求二元函数的定义域。

(2) 理解二元函数偏导数和全微分的概念。掌握二元函数的一阶、 二阶偏导数的求法，会求二元函数的全微分。

(3) 掌握复合函数一阶、二阶偏导数的求法。

(4) 掌握由方程F (x, y , z ) = 0 所确定的隐函数 z = f (x, y ) 的一阶偏导数的计算方法。

(5) 会求二元函数的无条件极值。

2.二重积分

二重积分的概念、性质。

二重积分的计算。

要求：

(1) 理解二重积分的概念、性质及其几何意义。

(2) 掌握二重积分在直角坐标系下的计算方法。

(五) 常微分方程 1.微分方程

微分方程的定义，微分方程的阶、解、通解、初始条件和特解。

可分离变量微分方程，一阶线性微分方程，二阶常系数齐次线性微分 方程。

要求：

(1) 理解微分方程的定义，理解微分方程的阶、解、通解、初始条 件和特解等概念。

(2) 掌握可分离变量微分方程的解法。

(3) 掌握一阶线性微分方程的解法。

(4) 掌握二阶常系数齐次线性微分方程的解法。

研究考试大纲，对大纲中的考点及相关要求进行认真研究，是应考的关键。正在备考专升本的同学，关注山东好老师升学帮网站可以了解更多专升本的考试信息。如果在学习上有困难，自制力差，可以在下方留下你的联系方式，我们的老师会针对你的学习情况给出建议。